Autores : Maria Eugência G. Porto
           Márcia M. C. Ferreira

 Departamento de Físico-Química / Instituto de Química / Ramal 8413

    Este trabalho tem como objetivo principal a apresentação do átomo de
 hidrogênio através de recursos gráfico, uma área que tem se desenvolvido
 bastante nos últimos tempos dentro da computação.
    Para isso, utilizaremos um software chamado Mathematica desenvolvido
 por Stephen Wolfram. Dividiremos o átomo de hidrogênio em partes radial e
 angular, para posteriormente apresentarmos a função de onda total.

          I) Parte radial do átomo de hidrogênio :
     A parte radial da função de onda descreve somente a relação da
 distância elétron-núcleo.
          R(n,l) = (r^l) exp[-zr/na] Polinômio de Laguerre

          II) Parte angular do átomo de hidrogênio :
     As auto-funções para a parte angular do átomo de hidrogênio são
 conhecidas como harmônicas esféricas :
 Y(l,m,theta,phi) = [(2l+1)(l-m)!/4Pi(l+m)!]P(l,m).Cos[theta].Exp[i m phi]

     No Mathematica os gráficos da harmônica esférica Y(2,0) ao quadrado,
 podem ser representados em coordenadas esféricas polares (Fig. I), e em
 coordenadas cartesianas (Fig. II).

          III) Função de onda total do átomo de hidrogênio :
     A função de onda total do átomo de hidrogênio pode ser definida como :
         para m=0 -> Y(n,l,m) = R(n.l) . Y(l,m)
         para m¹0 -> Y(n,l,m) = R(n.l) . [(-1) {Y(l,m) + Y(l,-m)}]
     Para respresentar funções de três variáveis independentes, r, theta,
 e phi (ou, x, y e z), seriam necessárias quatro dimensões. Fixando-se uma
 das variáveis igual a zero, pode-se observar dois tipos de gráficos para
 cada orbital, utilizando-se o Mathematica : curvas ou linhas de contorno
 isoprobabilísticas (Fig. III) e, superfícies tridimensionais (Fig. IV).

 Authors : Maria Eugência G. Porto
           Márcia M. C. Ferreira

 Departamento de Físico-Química / Instituto de Química / Ramal 8413

    The main purpose of this work is to present the hydrogen atom by means
 of graphical resources, an area that has been recently developed rather
 rapidly as a part of computing.
    Therefore, a software called Mathematica, developed by Stephen Wolfram,
 is used in this work. The hydrogen atom is divided into radial and angular
 parts, and then it is presented by the total wavefunction.
           I) The radial part of the hydrogen atom :
     The radial part of the wavefunction describes only the electron-
 nucleus distance.
          R(n,l) = (r^l) exp[-zr/na] Laguerre Polynomials

         II) The angular part of the hydrogen atom :
     The eigenfunctions for the angular part of the hydrogen atom are
 known as spherical harmonics :
 Y(l,m,theta,phi) = [(2l+1)(l-m)!/4Pi(l+m)!]P(l,m).Cos[theta].Exp[i m phi]

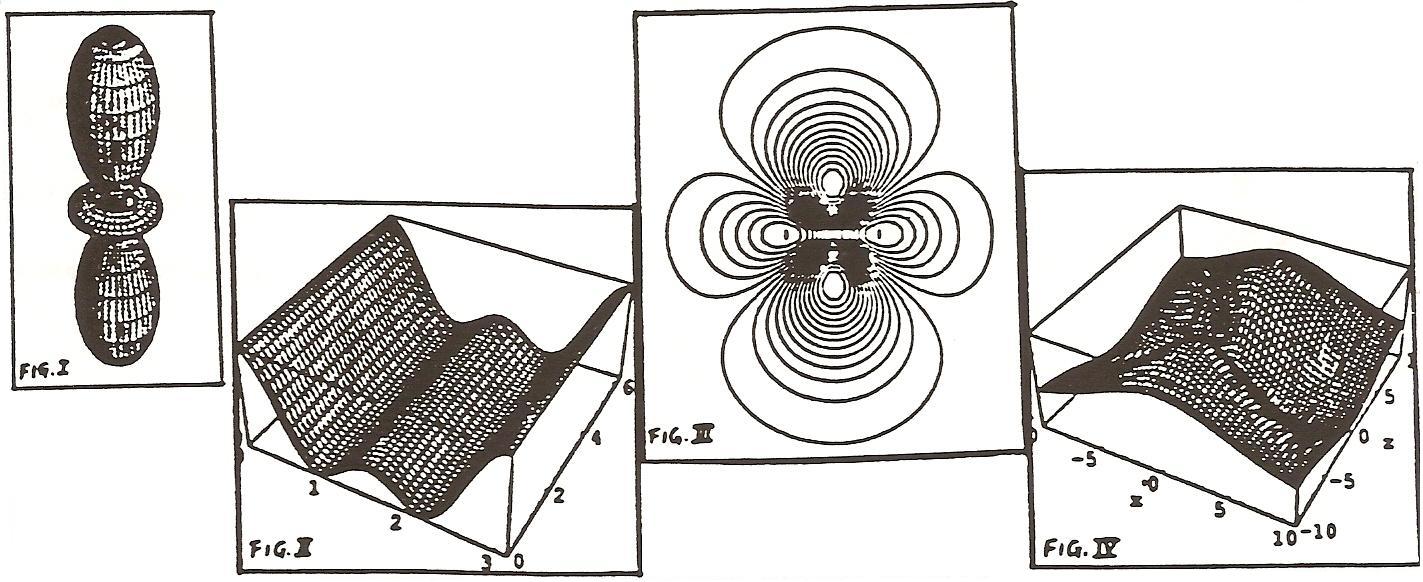
     In Mathematica, the graphs of the squared spherical harmonic Y(2,0) 
 can be represented in spherical polar coordinates (Fig. I), and in 
 Cartesian coordinates (Fig. II).

          III) The total  wavefunction of the hydrogen atom :
     The total wavefunction of the hydrogen atom can be defined as :
         for m=0 -> Y(n,l,m) = R(n.l) . Y(l,m)
         for m¹0 -> Y(n,l,m) = R(n.l) . [(-1) {Y(l,m) + Y(l,-m)}]
     To represent functions of three variables, r, theta, and phi (or, x,
 y, and z), four dimensions are necessary. By fixing a variable to zero,
 two types of graphs are obtained with Mathematica for each orbital :
 isoprobabilistic contour curves or lines  (Fig. III), and three-dimensi-
 onal surfaces (Fig. IV).